Logical Operators

Elementary trading algorithms are combined together through logical operators. They are described here.

Logical operators are defined first. Then each of the logical operators in Trading Conceiver is explained:

AND
OR
At least 2 (proprietary)
At least 3 (proprietary)

Finally, some examples of application are proposed.

Logical Operators

Definitions

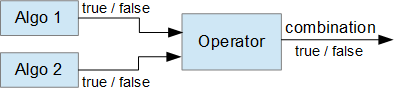The output of trading algorithms consists basically of the information of where the algorithm is true, i.e. satisfied, or false, i.e. not satisfied. Elementary trading algorithms make no exception. Logical operators, or Boolean operators, take the output of such algorithms and combine them according to some rules, specific to each operator. Such logic is called combinatorial. That's why we refer to the composition of trading algorithms as combination:

  combination = output_algorithm_1 logical_operator output_algorithm_2

The combination, i.e. the output of the operator, is still an algorithm, still consisting of true / false information. The various

  output_algorithm_n

are called the inputs or arguments of the operator.

Nomenclature: Input and Output

Just to be clear with the nomenclature about input and output. In a chain of processing, where each module makes some process and then gives the result to the next module for further processing, the output of the first module becomes the input of the second, but the data are exactly the same. In our case, the output of a trading algorithm is the input of the logical operator.

List of Operators

Trading Conceiver implements the following logical operators:

AND
OR
At least 2
At least 3

At Threshold

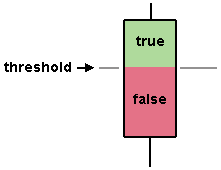Remember that at Threshold we must deal with intervals. At Threshold each elementary trading algorithm either is false, i.e. is true in the empty set, or is true in an interval. At Threshold, all the operators correspond to operations on intervals. That is the output of each operator corresponds to a specific operation on the intervals where the single elementary algorithms are true. Then the Boolean value of the output, that is the result of the operator, is set to true if the result of the operation between the intervals result in a non-empty interval; it is set to false otherwise.

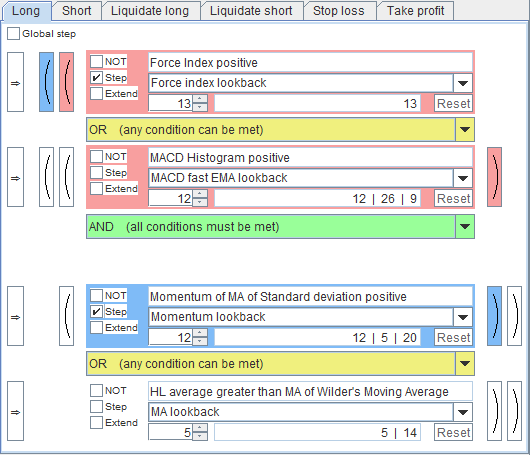
AND

Definition

The truth table of the AND logical operator is the following:


  input1  input2 │ output
  ───────────────┼───────
   false   false │ false
   false   true  │ false
   true    false │ false
   true    true  │ true

What it means is that the only way to make the output true is to have both inputs true. If we combine together two elementary trading algorithms through an AND operator, the combination of the two algorithms is satisfied only if they are both satisfied. In all other cases, the combination is false, i.e. not satisfied. If one of the two elementary trading algorithms is false, or both are, their combination is false, i.e. not satisfied.

More than Two Inputs: Associativity

The definition above holds for 2 inputs. It can be easily extended to the case of multiple inputs thanks to the associativity property of the Boolean AND operator, which states that we can AND together 2 inputs in any order and then AND the other inputs:

  input1 AND input2 AND input3 =
  = (input1 AND input2) AND input3 =
  = input1 AND (input2 AND input3)

By ANDing multiple arguments together, parentheses are thus uninfluential. In this case the output is true if and only if all three inputs are true, that is we require that all 3 conditions must be met simultaneously in order for the output to be true, or, said another way, that if even one input is false, the output is false.

When To Use It

The AND operator can be used to confirm a signal. It is known that it is a good practice to have multiple consistent signals, given by different and independent methods, in order to open or close a trade. When you want such confirmation, use the AND operator.

At Threshold: Intersection

The AND corresponds to the intersection of intervals:

  AND  ≡  ∩

That is the output of the AND operation corresponds to the intersection of the intervals where the single elementary algorithms are true:

  combination = 
    = algo_1  AND  algo_2  ≡
    ≡ algo_1   ∩   algo_2

Examples

algo_1 true in [a, b]
algo_2 true in [c, d]
combination = algo_1  AND  algo_2


         Example 1                           Example 2

      algo_1                                 algo_1
  ───╊━━━━━━╉─────────────>              ───╊━━━━━━╉───────>
     a      b                               a      b 
     ¦      ¦                               ¦      ¦
     ¦      ¦   algo_2                      ¦    algo_2
  ∩ ───────────╊━━━━━━╉───>              ∩ ─────╊━━━━━━╉───>
     ¦      ¦  c      d                     ¦   c  ¦   d
     ¦      ¦  ¦      ¦                     ¦   ¦  ¦   ¦
  = ──────────────────────>              = ─────╊━━╉───────>
     a      b  c      d                     a   c  b   d
   
    combination = false             combination = true in [c, b]

OR

Definition

The truth table of the OR logical operator is the following:


  input1  input2 │ output
  ───────────────┼───────
   false   false │ false
   false   true  │ true
   true    false │ true
   true    true  │ true

What it means is that it is enough that just one of the inputs to be true in order for the output to be true. If we combine together two elementary trading algorithms through an OR operator, the combination of the two algorithms is satisfied if just one of them, or both, is true. In the other case, i.e. if both the inputs are false, the output is false.

More than Two Inputs: Associativity

The definition above holds for 2 inputs. It can be easily extended to the case of multiple inputs thanks to the associativity property of the Boolean OR operator, which states that we can OR together 2 inputs in any order and then OR the other inputs:

  input1 OR input2 OR input3 =
  = (input1 OR input2) OR input3 =
  = input1 OR (input2 OR input3)

By ORing multiple arguments together, parentheses are thus uninfluential. In this case the output is true if and only if at least one input is true, that is we require that it is enough that just one condition is met in order for the output to be true, or, said another way, that the output is false only if all inputs are false.

When To Use It

If you are considering multiple algorithms giving trading signals and you want to trade when just one of those signals is triggered, use the OR operator. This way you might open or close a position as soon as possible, without waiting for confirmation by other signals.

At Threshold: Union

The OR corresponds to the union of intervals:

  OR  ≡  ∪

That is the output of the OR operation corresponds to the union of the intervals where the single elementary algorithms are true:

  combination = 
    = algo_1  OR  algo_2  ≡
    ≡ algo_1  ∪   algo_2

Examples

algo_1 true in [a, b]
algo_2 true in [c, d]
combination = algo_1  OR  algo_2


         Example 1                           Example 2

      algo_1                                 algo_1
  ───╊━━━━━━╉─────────────>              ───╊━━━━━━╉───────>
     a      b                               a      b 
     ¦      ¦                               ¦      ¦
     ¦      ¦   algo_2                      ¦    algo_2
  ∪ ───────────╊━━━━━━╉───>              ∪ ─────╊━━━━━━╉───>
     ¦      ¦  c      d                     ¦   c  ¦   d
     ¦      ¦  ¦      ¦                     ¦   ¦  ¦   ¦
  = ─╊━━━━━━╉──╊━━━━━━╉───>              = ─╊━━━━━━━━━━╉───>
     a      b  c      d                     a   c  b   d

combination = true in [a, b] ∪ [c, d]    combination = true in [a, d]

Multiple Intervals

Note that, like in the first example, an algorithm can be true not only in just one interval, but also in multiple intervals, or, more formally, in the union of intervals.

In the Table

In such cases, in the table, for simplicity, the union symbol (∪), is omitted.

At least 2

Definition

The proprietary 'At least 2' operator requires that at least two conditions must be satisfied between the ones selected as input in order to be true. In order to compute its output, the inputs with a true value are counted; if this count is greater than or equal to two, then the output is true:

  number of true input ≥ 2  <=>  output true

Otherwise the output is false. So this operator is inherently a multi-value input and makes sense only for 3 or more inputs. In Trading Conceiver you can choose between 3 or 4 input elementary algorithms.

Equivalence with AND

The At least 2 operator with just 2 inputs is equivalent to the AND operator. As the At least operator is substantially slower, always prefer the AND operator in this case:

  arg1 AND arg2

Rationale

This operator is something between the AND and the OR operators. With the AND operator you require that all conditions must be met. With the OR operator you require it is enough that just one condition must be met. With the At least 2 operator you require that two conditions must be met, without caring which. This way you have a confirmation of the signals, because at least 2 are consistent, which is safe, but are not waiting too long before trading, risking to be late, because you don't wait for all the signals to be consistent.

When To Use It

If you want to consider a few conditions for opening or closing a trade, and are looking for a compromise between staying safe and acting as soon as possible, consider using the At least 2 operator.

At Threshold

At Threshold, the At least 2 operator is true in those intervals where at least 2 algorithms are true. That is the output is true where the number of intersecting input intervals is greater than or equal to 2. If there are no at least 2 intervals intersecting where the input is true, then the output is false. Said another way, the output is true if there are at least 2 non-disjoint intervals among the input algorithms where the inputs are true.

Examples

algo_1 true in [a, b]
algo_2 true in [c, d]
algo_3 true in [e, f]
algo_4 true in [g, h]
Example 1:
  combination = algo_1  At_least_2  algo_2  At_least_2  algo_3
Example 2:
  combination = algo_1  At_least_2  algo_2  At_least_2  algo_3  At_least_2  algo_4


             Example 1                                    Example 2

     algo_1                                            algo_1
  ──╊━━━━━━╉─────────────────────>           ───╊━━━━━━━━━━━━━━━━━━━╉──────────>
    a      b                                    a                   b 
    ¦      ¦                                    ¦                   ¦
    ¦      ¦   algo_2                           ¦     algo_2        ¦
  ────────────╊━━━━━━╉───────────>           ───────╊━━━━━━━╉──────────────────>
    ¦      ¦  c      d                          ¦   c       d       ¦
    ¦      ¦  ¦      ¦                          ¦   ¦       ¦       ¦
    ¦      ¦  ¦      ¦   algo_3                 ¦   ¦       ¦       ¦   algo_3
  ──────────────────────╊━━━━━━╉─>           ───────────────────────────╊━━━╉──>
    ¦      ¦  ¦      ¦  e      f                ¦   ¦       ¦       ¦   e   f 
    ¦      ¦  ¦      ¦  ¦      ¦                ¦   ¦       ¦       ¦   ¦   ¦
  = ─────────────────────────────>              ¦   ¦    algo_4     ¦   ¦   ¦
     a     b  c      d  e      f             ───────────╊━━━━━━━╉──────────────>
                                                ¦   ¦   g       h   ¦   ¦   ¦
       combination = false                      ¦   ¦   ¦   ¦   ¦   ¦   ¦   ¦
                                           Σ  0 ¦ 1 ¦ 2 ¦ 3 ¦ 2 ¦ 1 ¦ 0 ¦ 1 ¦ 0
                                           =   ─────╊━━━━━━━━━━━╉──────────────>
                                                a   c   g   d   h   b   e   f
         
                                                  combination = true in [c, h]

In example 2, the row denoted by 'Σ' indicates, for each sub-interval, the number of intersecting input intervals. The output is true where this number is ≥ 2.

Parentheses

When, in the same tab, another operator is present in addition to the At least 2 operator, all inputs (arguments) to the At least 2 operator must be enclosed in parentheses.

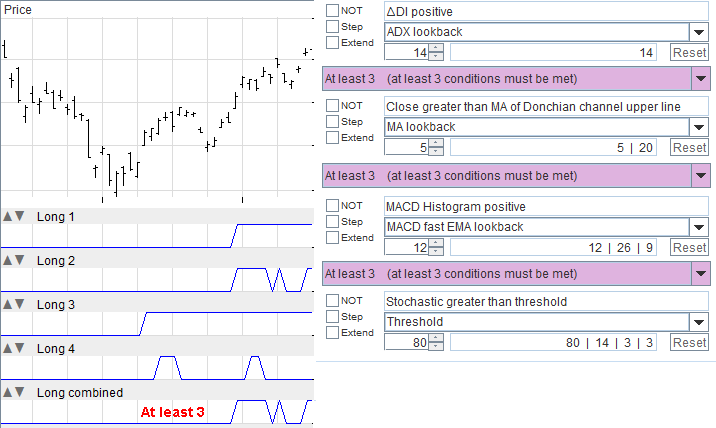
At least 3

This proprietary operator is exactly like the At least 2 operator, but requires that at least three conditions must be met. Refer to the previous paragraph, with the following observations. This operator makes sense only for 4 or more inputs. In Trading Conceiver you must choose 4 input elementary algorithms, filling up all one tab.

Equivalence with AND

The At least 3 operator with just 3 inputs is equivalent to the AND operator. As the At least operator is substantially slower, always prefer the AND operator in this case:

  arg1 AND arg2 AND arg3

Rationale

This operator tends toward a safer side with respect to the At least 2 operator, because an extra confirmation is required. However, the signal will be given later.

Examples of Application

AND: Confirmation with Long-Term Trend

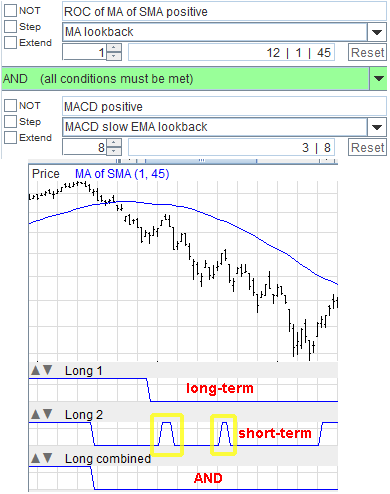Let's suppose you want to enter a long position according to some conditions of your choice, but only when the market is uptrending in the long term. As an uptrend long-term indicator you can select:

  ROC of MA of SMA positive

and set the lookback input parameters according to what 'long' means for you in this case. Then you AND this algorithm with the one of your choice; it will act as a confirmation signal. In the example, you can see the short-term algorithm giving long signals even when the long-term trend is negative, which is bad, because they would probably lead to loosing trades. The long-term signal is false, and by ANDing the algorithms together the overall signal is false; thus you correctly ignore the short-term signals in this phase of the market.

Other examples are presented in the chapter 'Algorithms from Base Indicators'.

OR: Liquidate as Soon as Possible

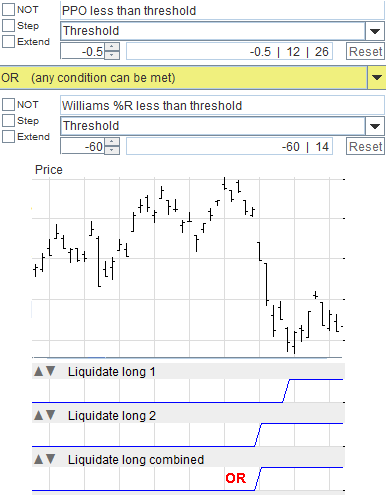Suppose you want to liquidate a long position as soon as possible when the market trend changes. You spotted some conditions that you like, and want to liquidate as soon as the first condition signaling to liquidate is satisfied. You can OR those conditions together. One of the two conditions is satisfied well before the other, and the overall signal is given right away, without waiting for the late signal.

At least 2: Soon Enough but Safe

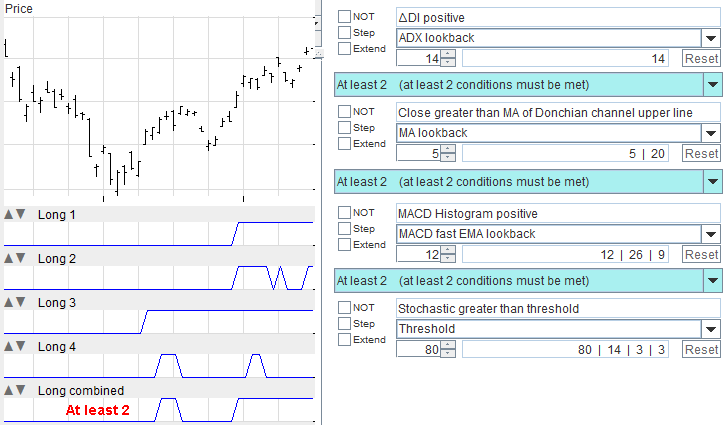
Suppose you pinpointed 4 algorithms you like to follow and you 'trust' them the same way. You can open a long position when two of them are true, confirming each other, without waiting for all 4 conditions to be met, which could happen too late. So you can use the At least 2 operator. In the example you can see that one of the algorithms gives the signal before all the others, which might prove wrong. It is only when a second signal gives its approval that the At least 2 becomes true and you can open a long position. At a certain point, all conditions are satisfied, but that comes after a while, and that could cause an overdue sign, with loss of profit.

At least 3: Soon Enough and Safer

By using the same algorithms as in the previous example, we can see the differences by applying the At least 3 operator. Notice how the signal is given later than in the case of the At least 2 operator, but gives a safer signal.